一句话总结

来自 Meta 和 MIT 的邓明阳、李赫、李天虹、杜一伦和何恺明提出了一种名为“漂移模型”的新生成范式，该范式在训练过程中通过漂移场演化前推分布，实现单步推理，并在 ImageNet 256×256 上取得最先进的 FID 分数。

主要贡献

• 漂移模型引入了一种新生成范式，通过漂移场在训练过程中演化前推分布，实现无需迭代采样或依赖 SDE/ODE 动力学的单步推理。
• 该方法使用一种新颖的目标函数训练单通神经网络，通过对比数据分布与生成分布以最小化样本漂移，当分布匹配时达到平衡。
• 在 ImageNet 256×256 上，该方法在潜在空间中达到 1.54、像素空间中达到 1.61 的最先进单步 FID 分数，优于先前的单步及许多多步生成模型。

引言

作者利用一种名为“漂移模型”的新颖训练时分布演化框架，通过学习一个单通生成器，使其在优化过程中收敛到数据分布，从而消除对迭代推理的需求。与依赖 SDE/ODE 求解器的扩散或流模型不同，漂移模型定义了一个漂移场，在训练期间将生成样本推向真实数据，当分布匹配时漂移停止。先前的单步方法要么蒸馏多步模型，要么近似动力学，而漂移模型引入了一种直接、非对抗性、非基于 ODE 的目标函数，通过类似对比学习的正负样本最小化样本漂移——在 ImageNet 256×256 上实现最先进的 1-NFE FID 分数：潜在空间 1.54，像素空间 1.61。

数据集

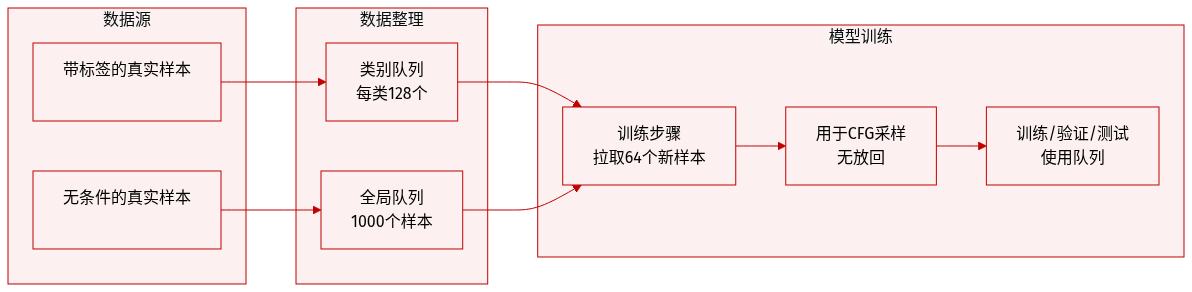
• 作者使用样本队列系统存储和检索真实（正/无条件）训练数据，模仿专用数据加载器的行为，同时借鉴了 MoCo 的队列设计。
• 对于每个类别标签，一个大小为 128 的队列存储带标签的真实样本；一个大小为 1000 的全局队列存储用于无分类器引导（CFG）的无条件样本。
• 在每个训练步骤中，最新的 64 个真实样本（带标签）被推入各自的队列，最旧的样本被移除以保持队列大小固定。
• 在采样时，正样本从类别特定队列中无放回抽取，无条件样本来自全局队列。
• 此方法确保统计一致的采样，同时避免自定义数据加载器的复杂性，尽管作者指出后者更符合原理。

方法

作者利用一种名为“漂移模型”的新颖生成建模框架，将训练概念化为通过漂移场迭代演化前推分布的过程。其核心是定义一个神经网络 $f_\theta: \mathbb{R}^C \mapsto \mathbb{R}^D$fθ​:RC↦RD，将噪声样本 $\epsilon \sim p_\epsilon$ϵ∼pϵ​ 映射到生成输出 $\mathbf{x} = f_\theta(\epsilon) \sim q$x=fθ​(ϵ)∼q，其中 $q = f_{\#}p_\epsilon$q=f#​pϵ​ 表示前推分布。训练目标是通过最小化漂移场 $\mathbf{V}_{p,q}(\mathbf{x})$Vp,q​(x) 使 $q$q 与数据分布 $p_{\text{data}}$pdata​ 对齐，该场控制每个样本 $\mathbf{x}$x 在每个训练迭代中应如何移动。

漂移场被设计为诱导固定点平衡：当 $q = p$q=p 时，该场处处消失，即 $\mathbf{V}_{p,q}(\mathbf{x}) = \mathbf{0}$Vp,q​(x)=0。这一特性启发了一种从固定点迭代推导出的训练损失：在第 $i$i 次迭代中，模型更新其预测以匹配通过漂移当前样本计算出的冻结目标，从而得到损失函数：

$$\mathcal{L} = \mathbb{E}_{\epsilon} \left[ \left\| f_{\theta}(\epsilon) - \mathrm{stopgrad}\left( f_{\theta}(\epsilon) + \mathbf{V}_{p,q_{\theta}}\left( f_{\theta}(\epsilon) \right) \right) \right\|^2 \right].$$L=Eϵ​[∥fθ​(ϵ)−stopgrad(fθ​(ϵ)+Vp,qθ​​(fθ​(ϵ)))∥2].

该公式通过在每一步冻结分布依赖场 $\mathbf{V}$V 的值，避免了通过 $\mathbf{V}$V 的反向传播，从而间接最小化漂移向量 $\mathbf{V}$V 的平方范数。

漂移场 $\mathbf{V}_{p,q}(\mathbf{x})$Vp,q​(x) 通过基于核的吸引-排斥机制实例化。它被分解为两个部分：$\mathbf{V}_p^+(\mathbf{x})$Vp+​(x) 将 $\mathbf{x}$x 吸引向数据样本 $\mathbf{y}^+ \sim p$y+∼p，$\mathbf{V}_q^-(\mathbf{x})$Vq−​(x) 将 $\mathbf{x}$x 排斥远离生成样本 $\mathbf{y}^- \sim q$y−∼q。净漂移计算为 $\mathbf{V}_{p,q}(\mathbf{x}) = \mathbf{V}_p^+(\mathbf{x}) - \mathbf{V}_q^-(\mathbf{x})$Vp,q​(x)=Vp+​(x)−Vq−​(x)。下图展示了生成样本 $\mathbf{x}$x（黑点）如何被拉向数据分布（蓝点）并被推离当前生成分布（橙点）。

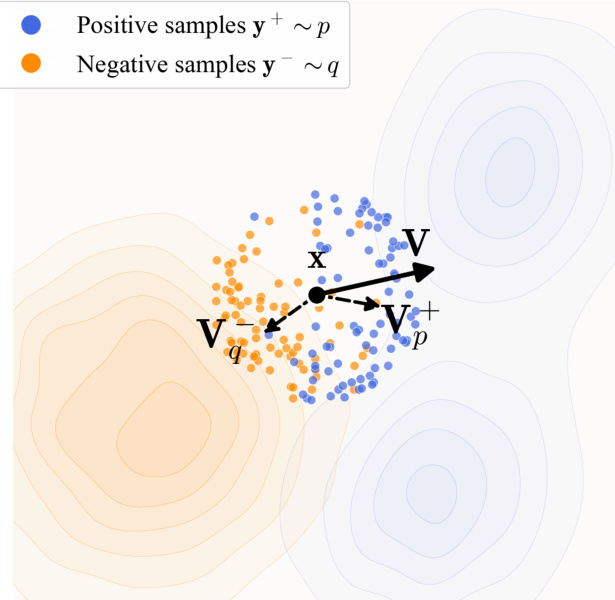
在实践中，该场使用归一化核 $k(\mathbf{x}, \mathbf{y}) = \exp(-\frac{1}{\tau} \|\mathbf{x} - \mathbf{y}\|)$k(x,y)=exp(−τ1​∥x−y∥) 计算，通过批次内成对距离的 softmax 实现。核在正负样本上联合归一化，确保场满足反对称性 $\mathbf{V}_{p,q} = -\mathbf{V}_{q,p}$Vp,q​=−Vq,p​，从而在 $p = q$p=q 时保证平衡。实现中还包含对批次内生成样本的第二次归一化以提高稳定性。

为了提升性能，作者将漂移损失扩展到特征空间，使用预训练的自监督编码器（例如 ResNet、MAE）。损失在特征图的多个尺度和空间位置上计算，每个特征独立归一化以确保跨不同编码器和特征维度的鲁棒性。总体损失聚合所有特征的贡献，按归一化漂移向量加权。

对于条件生成，该框架通过将无条件数据样本混合到负样本集中自然支持无分类器引导，有效地训练模型以近似条件和无条件分布的线性组合。该引导仅在训练时应用，保留推理时的单步（1-NFE）生成特性。

生成器架构遵循 DiT 风格的 Transformer，采用基于块的标记化、adaLN-zero 条件化和可选的随机风格嵌入。训练在潜在空间中使用 SD-VAE 标记器进行，必要时通过 VAE 解码器在像素空间中提取特征。模型使用随机小批量优化训练，每个批次包含生成样本（作为负样本）和真实数据样本（作为正样本），漂移场在这些集合上经验计算。

实验

• 玩具实验表明，该方法即使从崩溃的初始化出发，也能避免模式崩溃，允许样本被吸引到目标分布的未充分表示的模式。
• 漂移场的反对称性至关重要；破坏它会导致灾难性失败，证实其在实现 p 和 q 之间平衡中的作用。
• 在固定计算预算下增加正负样本数量可提高生成质量，符合对比学习原则。
• 特征编码器质量显著影响性能；潜在 MAE 优于标准 SSL 编码器，更宽和更长训练的变体带来进一步提升。
• 在 ImageNet 256×256 上，该方法实现最先进的 1-NFE FID 分数（潜在空间 1.54，像素空间 1.61），优于多步和基于 GAN 的单步方法，同时使用更少的 FLOPs。
• 像素空间生成比潜在空间更具挑战性，但受益于更强大的编码器（如 ConvNeXt-V2）和扩展训练。
• 在机器人控制任务中，单步漂移模型匹配或超过 100-NFE 扩散策略，展示跨领域适用性。
• 核归一化提升性能，但非严格必要，即使未归一化的变体也能避免崩溃并保持合理结果。
• CFG 尺度在 FID 和 IS 之间权衡，类似于扩散模型；最优 FID 出现在 α=1.0，等同于标准框架中的“无 CFG”。
• 生成图像在训练数据中与其最近邻明显不同，表明新颖性而非记忆。

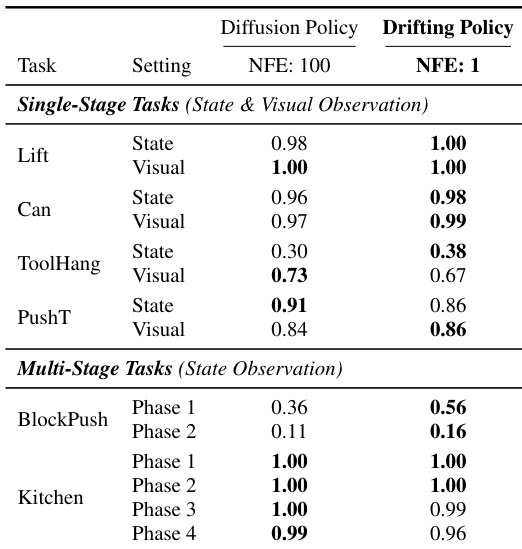
作者在机器人控制任务上评估其单步漂移策略，替代 Diffusion Policy 的多步生成器。结果表明，该方法在单阶段和多阶段任务中均匹配或超过 100 步 Diffusion Policy 的性能，证明其作为机器人领域生成模型的有效性。

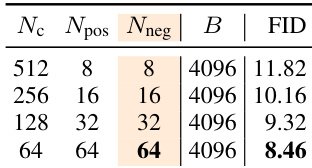
作者证明，在固定计算预算下增加负样本数量可提高生成质量（FID 分数更低）。这与更大样本集能更准确估计漂移场、推动生成器更好对齐目标分布的观察一致。该趋势在不同配置中均成立，强化了样本多样性对训练稳定性和性能的重要性。

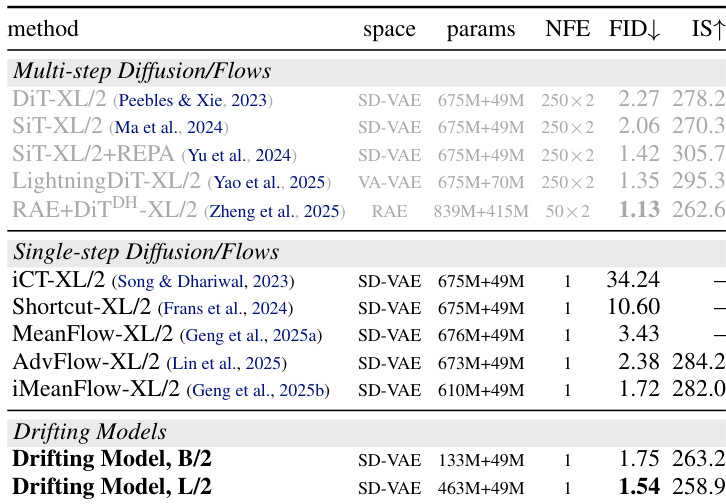
作者在 ImageNet 256×256 上将漂移模型与多步和单步扩散/流方法进行比较，显示其单步方法在仅需单次网络函数评估的情况下实现竞争性或更优的 FID 分数。结果表明，更大的模型尺寸提升性能，L/2 变体在无无分类器引导的情况下达到最先进的 1.54 FID。该方法优于先前的单步生成器，并在质量上匹配或超过多步模型，尽管计算效率更高。

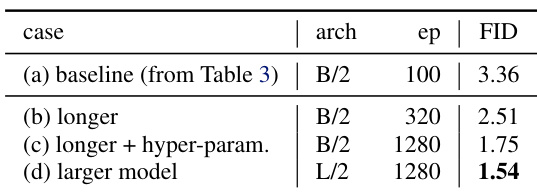
作者证明，延长训练时间和调整超参数显著提升生成质量，FID 从 3.36 降至 1.75。扩大模型尺寸进一步将 FID 降至 1.54，表明架构容量和训练规模是其框架性能的关键驱动因素。

作者证明，延长训练时间和扩大模型尺寸显著提升生成质量，FID 在受控条件下从 3.70 逐步降至 1.61。这些改进未改变核心方法，表明性能提升源于更大容量和更长优化，而非架构变更。