Command Palette
Search for a command to run...
迈向自主数学研究
迈向自主数学研究
摘要
近年来,基础模型的快速发展催生了具备国际数学奥林匹克竞赛金牌水平推理能力的系统。然而,从竞赛级问题求解向专业数学研究的过渡,仍需应对海量文献的梳理以及长周期、复杂链条的证明构建。在本研究中,我们提出了Aletheia——一个数学研究代理(math research agent),其能够在自然语言环境中端到端地迭代生成、验证与修订数学解题方案。具体而言,Aletheia依托于改进版的Gemini Deep Think模型,以应对高难度推理任务;引入一种新颖的推理时扩展规律(inference-time scaling law),将能力延伸至超越奥数级别的问题;并通过高强度工具调用,有效应对数学研究中的复杂性挑战。我们展示了Aletheia从奥数题到博士级别习题的广泛适用性,并在人工智能辅助数学研究领域实现了多个重要里程碑:(a)由AI完全自主生成的一篇研究论文(Feng26),无需任何人工干预,计算了算术几何中一类称为“特征权重”(eigenweights)的结构常数;(b)另一篇论文(LeeSeo26),展示了人类与AI协同合作,在证明“独立集”(independent sets)系统中相互作用粒子的界方面取得突破;(c)对Bloom的Erdős猜想数据库中700个开放问题的广泛半自主评估(Feng et al., 2026a),其中AI自主解决了其中四个长期悬而未决的问题。为进一步促进公众对人工智能与数学融合发展进程的理解,我们建议建立标准化的评估层级体系,用于量化人工智能辅助成果在自主性与新颖性方面的水平。最后,本文对数学领域中人机协作的未来发展方向进行了深入反思。
一句话总结
Google DeepMind 的研究人员推出了 Aletheia,这是一种由 Gemini Deep Think 和新型推理扩展技术驱动的数学研究代理,能够端到端地生成、验证和修订自然语言证明;它自主解决了多个开放的 Erdős 问题,生成了研究论文,并展示了在高级数学发现中人机协作的能力。
主要贡献
- Aletheia 引入了一种自主数学研究代理,通过迭代生成、验证和修订自然语言证明,填补了竞赛级问题求解与开放式研究之间的鸿沟,整合了高级推理、推理时扩展和工具使用(如网络搜索)。
- 该系统在奥林匹克竞赛基准测试中取得最先进性能(IMO-ProofBench 达 95.1%),并在博士级练习中表现出色,通过自主解决四个 Erdős 开放问题并产出一篇关于算术几何中特征权的完全由 AI 生成的论文,展示了真实的研究影响力。
- Aletheia 支持在证明独立集界值时的人机协作,并参与多篇研究论文,同时作者提出了一种标准化分类法,用于界定 AI 在数学成果中的自主性和新颖性,以提升透明度和公众理解。
引言
作者利用大型语言模型的最新进展,弥合竞赛级数学问题求解与专业数学研究之间的差距,后者要求综合大量文献并构建长程证明——此前模型常因幻觉和浅层领域理解而失败。他们引入 Aletheia,一种数学研究代理,通过增强的 Gemini Deep Think 模型、新型推理时扩展定律及工具集成(如网络搜索),迭代生成、验证并修订解决方案。Aletheia 在奥林匹克竞赛、博士级及开放研究问题上均展现出能力,包括自主推导算术几何中的结构常数、与人类合著粒子系统证明,以及半自主解决四个 Erdős 猜想——标志着迈向可扩展 AI 辅助数学发现的第一步。
方法
作者采用一个多代理协调框架(内部代号为 Aletheia),应对自主数学研究的挑战。该框架基于 Gemini Deep Think 构建,旨在克服大型语言模型在处理高级研究级数学问题时的局限性——这类问题通常需要深厚的领域知识和超出标准竞赛题范围的严格验证。
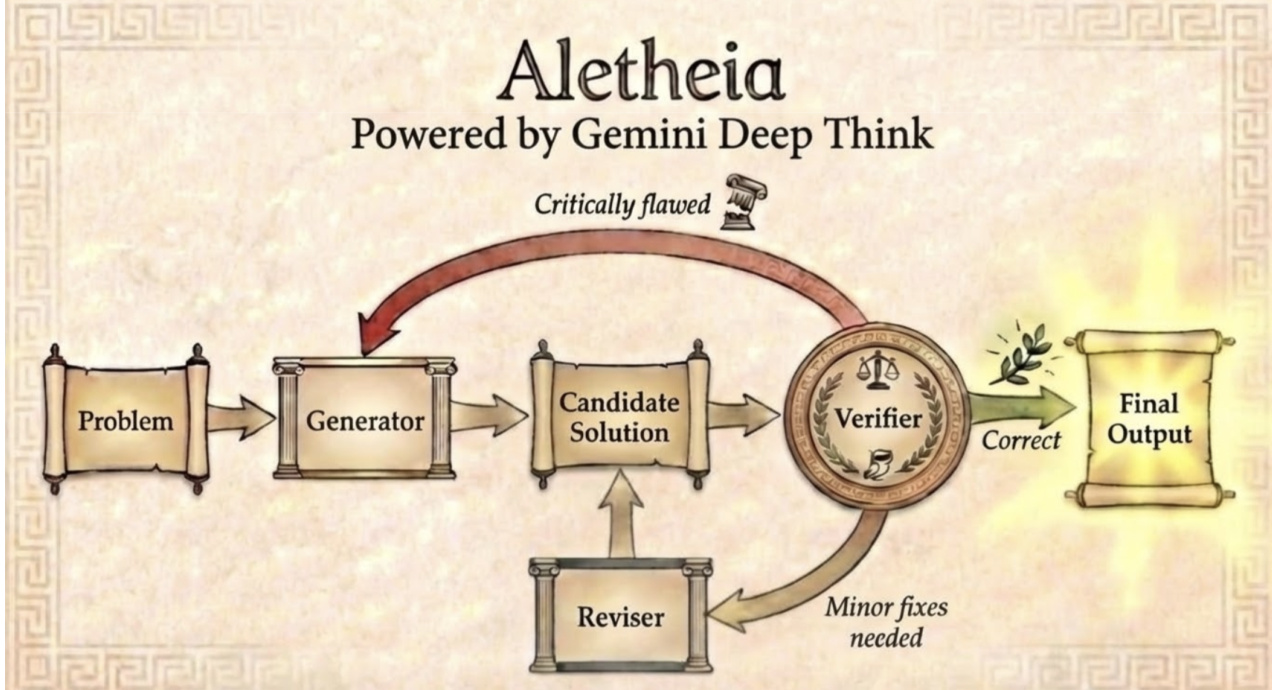
Aletheia 的核心架构由三个紧密耦合的子代理组成:生成器(Generator)、验证器(Verifier)和修订器(Reviser)。生成器负责为给定数学问题生成初始候选解;这些候选解随后传递给验证器,后者对其正确性和逻辑严密性进行批判性评估。若验证器发现缺陷,则将候选解返回修订器,由其进行针对性改进或微调。此迭代循环持续进行,直到验证器批准解决方案或达到预设尝试上限。整个流程旨在模拟人类数学家的猜想、批判与修订循环。
请参阅框架图,该图展示了子代理间的信息与控制流。生成器接收问题陈述并生成候选解,验证器随后评估该解,要么批准其作为最终输出,要么标记为需修订。修订器收到反馈后修改候选解,并重新提交给生成器以供再评估。这种闭环设计确保解决方案不仅被生成,还经过严格验证与精炼,显著提升输出的可靠性。
实验
- Gemini Deep Think 通过解决 2025 年六道题中的五道,达到 IMO 金牌水平,展示了在推理扩展下的强劲表现,准确率在达到平台期前显著提升。
- 更高效的模型(2026 年 1 月版)将计算需求降低 100 倍,同时维持或提升性能,高扩展下解决了包括 2024 年 P3 和 P5 在内的难题,但知识截止日期可能引发暴露风险。
- 在 FutureMath(博士级数学)上,性能在低于 IMO 的准确率下饱和,专家反馈指出持续存在的幻觉和错误限制了研究实用性,尽管进行了扩展。
- 工具使用(尤其是网络搜索)显著减少了 Aletheia 的引用幻觉,但对真实论文的细微误述仍存在;Python 集成贡献甚微,表明基础数学能力已较高。
- 在测试 700 个 Erdős 问题时,Aletheia 生成了 212 个候选解;63 个技术上正确,但仅 13 个有意义地解决了原问题——其中 4 个代表自主或部分自主的新解。
- 消融研究表明,Gemini Deep Think(IMO 规模)在 Aletheia 解决的 13 个 Erdős 问题中解决了 8 个,使用两倍计算量,并部分复现了研究论文结果,表明 Aletheia 的工具增强方法超越了纯扩展的价值。
- AI 仍易误解模糊问题、偏向平凡解、幻觉或误引文献——即使使用工具——揭示其在创造力、深度和可靠性方面与人类研究员的定性差距。
- 多数 AI 生成的数学成果简短且基础;成功常源于技术操作或检索,而非概念创新,人类监督对新颖性和严谨性仍至关重要。
- 当被提示将解调整至 IMO 标准时,模型成功用初等技术重写证明,达到完全严谨——显示其在约束下的适应性,尽管初始尝试依赖未经证实的高级定理。
- 在 IMO 2024 变体题中,模型在 2^7 规模下解决第 3 题(含微小错误),在 2^8 规模下解决第 5 题,使用新颖的、非视觉的、基于状态的推理——暗示从第一性原理推导而非记忆。
结果显示,在评估 200 个开放 Erdős 问题的候选解时,多数根本错误,仅一小部分在技术和意义上均正确。模型常生成在宽松解释下数学上有效但未解决原定数学意图的解,突显其对问题背景理解的持续差距。即使有验证机制,系统仍易误读和幻觉,限制其在自主研究中的可靠性。
