Command Palette
Search for a command to run...
Learning to Discover at Test Time
Learning to Discover at Test Time
Abstract
How can we use AI to discover a new state of the art for a scientific problem? Prior work in test-time scaling, such as AlphaEvolve, performs search by prompting a frozen LLM. We perform reinforcement learning at test time, so the LLM can continue to train, but now with experience specific to the test problem. This form of continual learning is quite special, because its goal is to produce one great solution rather than many good ones on average, and to solve this very problem rather than generalize to other problems. Therefore, our learning objective and search subroutine are designed to prioritize the most promising solutions. We call this method Test-Time Training to Discover (TTT-Discover). Following prior work, we focus on problems with continuous rewards. We report results for every problem we attempted, across mathematics, GPU kernel engineering, algorithm design, and biology. TTT-Discover sets the new state of the art in almost all of them: (i) Erdős' minimum overlap problem and an autocorrelation inequality; (ii) a GPUMode kernel competition (up to faster than prior art); (iii) past AtCoder algorithm competitions; and (iv) denoising problem in single-cell analysis. Our solutions are reviewed by experts or the organizers. All our results are achieved with an open model, OpenAI gpt-oss-120b, and can be reproduced with our publicly available code, in contrast to previous best results that required closed frontier models. Our test-time training runs are performed using Tinker, an API by Thinking Machines, with a cost of only a few hundred dollars per problem.
One-sentence Summary
Stanford, NVIDIA, and collaborators propose TTT-Discover, a test-time training method enabling LLMs to continually learn on single problems via reinforcement learning, outperforming prior frozen-model approaches across math, GPU kernels, algorithms, and biology—using open models and low-cost computation.
Key Contributions
- TTT-Discover introduces test-time reinforcement learning for scientific discovery, enabling large language models to adapt their parameters during inference to solve a single hard problem—unlike prior frozen-model search methods—by prioritizing the most promising solutions through a tailored learning objective.
- The method achieves state-of-the-art results across diverse domains including mathematics (Erdős’ minimum overlap, autocorrelation inequalities), GPU kernel engineering (2× faster than prior art), algorithm design (AtCoder), and biology (single-cell denoising), with solutions validated by domain experts or competition organizers.
- All results are reproducible using the open model OpenAI gpt-oss-120b and publicly available code, at a cost of only a few hundred dollars per problem via the Tinker API, contrasting with prior SOTA methods that relied on closed, proprietary models.
Introduction
The authors leverage test-time reinforcement learning to enable large language models to continuously improve while solving a single, specific scientific problem—rather than relying on static prompting or evolutionary search. This approach matters because many discovery tasks require novel solutions beyond existing knowledge, where generalization from training data fails. Prior methods, like AlphaEvolve, search the solution space with frozen models using hand-crafted heuristics, limiting the model’s ability to internalize new strategies. TTT-Discover’s key contribution is a tailored RL framework that optimizes for one high-reward solution per problem, using an entropic objective and PUCT-based search to prioritize promising candidates. It achieves state-of-the-art results across math, GPU kernel design, algorithm contests, and biology—all with an open model and low cost—outperforming concurrent methods like ThetaEvolve under identical conditions.

Dataset
The authors use the OpenProblems benchmark for single-cell RNA-seq denoising, which includes three datasets: PBMC, Pancreas, and Tabula Muris Senis Lung, ordered by size. They train their policy on the Pancreas dataset and evaluate final performance on PBMC and Tabula Muris Senis Lung, using held-out test sets created via binomial sampling to simulate ground truth.
Key processing steps include:
- Converting input matrices to float64 and preserving raw library sizes for reverse normalization.
- Applying variance-stabilizing transforms (e.g., Anscombe) and library-size normalization.
- Selecting highly variable genes (HVGs) to reduce dimensionality.
- Re-normalizing after imputation to maintain stochastic properties.
The denoising task evaluates algorithms using two metrics: mean squared error in log-normalized space (primary reward) and Poisson negative log-likelihood (constraint). Algorithms are penalized if they exceed 400 seconds or violate Poisson score constraints.
The authors compare their method against MAGIC (state-of-the-art), ALRA, OpenEvolve, and Best-of-25600, using the same evaluation framework to ensure fair comparison.
Method
The framework of the proposed method, TTT-Discover, is designed to address discovery problems at test time by leveraging a large language model (LLM) policy to iteratively improve solutions through online learning and strategic state reuse. The overall architecture operates within a reinforcement learning (RL) paradigm, where the policy πθ is trained on its own search attempts accumulated in a buffer Hi, enabling continuous improvement during the discovery process. The method begins with an initial state si, which is sampled from the buffer Hi using a reuse heuristic that prioritizes high-reward solutions while maintaining exploration. The policy then generates an action ai∼πθ(⋅∣d,si,ci), where d is the problem description and ci is a context derived from previous actions, if applicable. The environment transitions to a new state si′=T(ai), and the reward ri=R(si′) is evaluated. This attempt is added to the buffer Hi+1, and the policy weights θi are updated using a specialized training objective.
The core innovation lies in the design of the training objective and the reuse heuristic. The training objective is an entropic utility objective Jβ(θ), which is defined to favor actions that lead to high rewards by reweighting the policy gradient update based on the exponential of the reward scaled by a temperature parameter β(s). This objective is formulated as Jβ(θ)=Es∼reuse(H)[logEa∼πθ(⋅∣s)[eβ(s)R(s,a)]], with the gradient update ∇θJβ(θ)=Es∼reuse(H)[wβ(s)(a)∇θlogπθ(a∣s)], where wβ(s)(a) is the normalized exponential weight. To ensure stability and adaptability, β(s) is set adaptively per initial state by constraining the KL divergence between the original policy and the tilted distribution induced by the entropic weights, ensuring the update does not deviate too far from the current policy.
The reuse heuristic is inspired by the PUCT (Policy, Uncertainty, and Tree Search) algorithm, adapted for state selection from a buffer of previously discovered solutions. Each state s in the buffer Hi is scored by a PUCT-inspired rule: score(s)=Q(s)+c⋅scale⋅P(s)⋅1+T/(1+n(s)). Here, Q(s) represents the maximum reward achieved from any child state generated when s was the initial state, capturing the optimistic potential of the state. P(s) is a linear rank-based prior, favoring high-reward states, while the exploration bonus term 1+T/(1+n(s)) discourages over-exploitation by reducing the score of frequently selected states. This mechanism ensures a balance between exploiting promising states and exploring under-visited ones, which is crucial for discovering novel solutions.
The method is instantiated in Algorithm 1, which outlines the test-time training process. It initializes the buffer with the empty solution and iteratively samples an initial state and context, generates an action, transitions to a new state, evaluates the reward, updates the buffer, and trains the policy. The key difference from standard RL is the objective: instead of optimizing for average performance, TTT-Discover optimizes for the maximum reward, which aligns with the goal of finding a single state that surpasses the state-of-the-art. This is achieved through the entropic objective, which effectively shifts the focus from expected reward to the probability of achieving high-reward outcomes. The combination of this objective with the PUCT-based reuse heuristic enables the method to efficiently explore the solution space, extend the effective horizon by reusing previous solutions, and discover significant improvements.
Experiment
- TTT-Discover with gpt-oss-120b on Tinker (50 steps, 512 rollouts/step) sets new state-of-the-art in Erdős’ Minimum Overlap Problem (bound 0.380876, surpassing AlphaEvolve’s 0.380924) and First Autocorrelation Inequality (C₁ ≤ 1.50286), using asymmetric 600-piece and 30,000-piece step functions respectively; outperforms Best-of-25600 and OpenEvolve baselines.
- On Autocorrelation Inequality C₂, TTT-Discover achieves 0.959 (vs. AlphaEvolve’s 0.961); on Circle Packing (n=26,32), matches best known with Qwen3-8B but no improvement.
- In GPU kernel engineering (TriMul), TTT-Discover kernels achieve 15–50% speedups over top human submissions across H100, A100, B200, MI300X; fuses operations, uses FP16 + cuBLAS/rocBLAS; MLA-Decode kernels underperform human top submissions on MI300X.
- In AtCoder Heuristic Contests, TTT-Discover wins 1st place in ahc039 (starting from ALE-Agent’s 5th-place solution) and ahc058 (from scratch), outperforming ALE-Agent and ShinkaEvolve despite using smaller model budgets.
- In single-cell denoising (OpenProblems), TTT-Discover improves MSE over MAGIC baseline on Pancreas dataset and generalizes to pbmc/tabula; adds gene-adaptive transforms, SVD refinement, log-space polishing.
- Ablations show full TTT-Discover (entropic objective + PUCT reuse) is essential; constant β, no entropic objective, or no reuse degrade performance; Best-of-25600 baseline improves Erdős bound but not consistently across tasks.
The authors use TTT-Discover with adaptive entropic objective and PUCT reuse to achieve the best runtime of 1203.10 microseconds in the TriMul kernel optimization task. Ablations show that removing the entropic objective or reuse method significantly degrades performance, while the full TTT-Discover setup outperforms both naive RL and Best-of-N baselines.
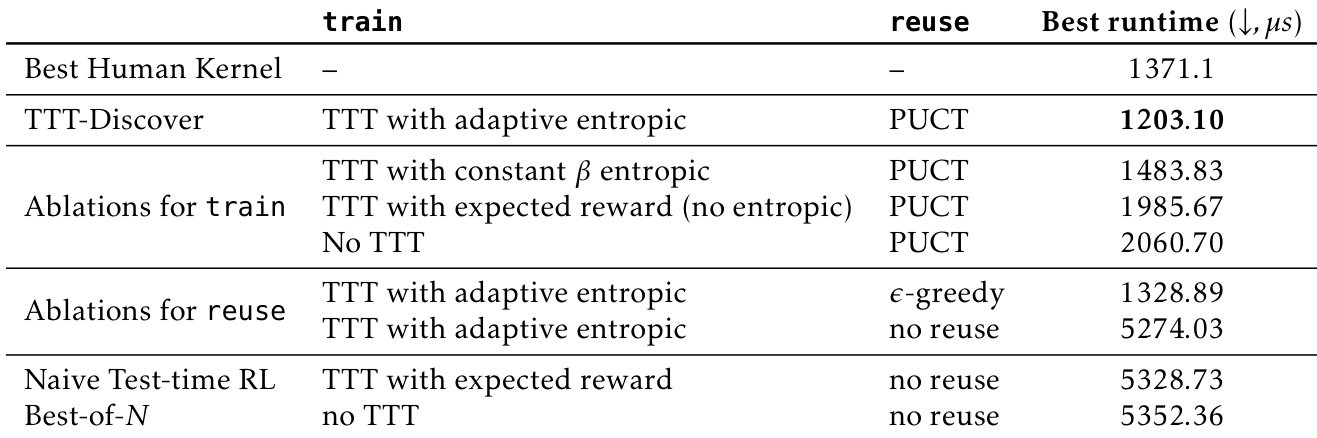
Results show that TTT-Discover achieves a mean runtime of 1669.1 microseconds on AMD MI300X, outperforming the best human submission (2038.6 microseconds) and the Best-of-25600 baseline (2286.0 microseconds). The method demonstrates consistent performance across all three instances, with 95% confidence intervals indicating statistically significant improvements over human and baseline results.
Results show that TTT-Discover with Qwen3-8B achieves the same performance as AlphaEvolve V2 and ShinkaEvolve on the circle packing task for n=26 and n=32, matching the best known results without improvements.
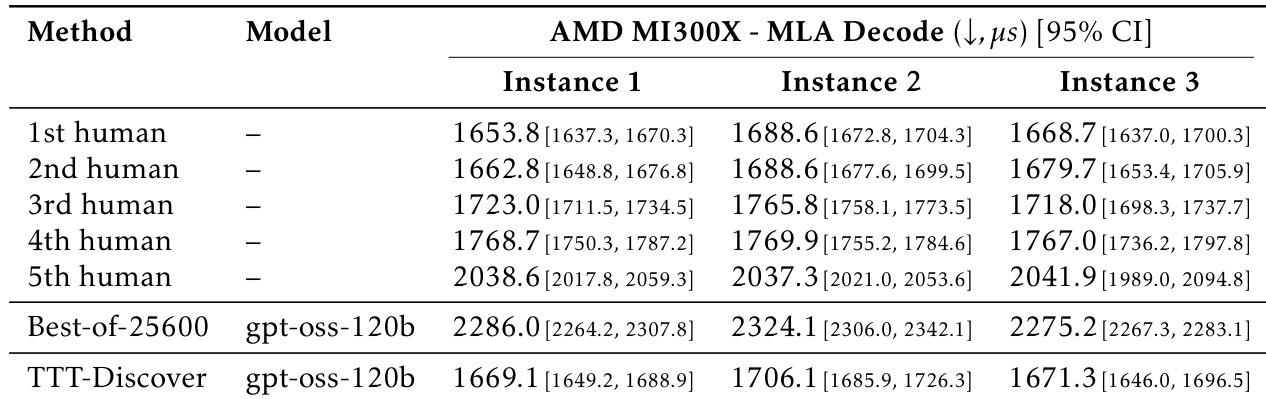
Results show that TTT-Discover achieves the highest score in both the Geometry (ahc039) and Scheduling (ahc058) competitions, outperforming all human submissions and prior AI baselines. In Geometry, TTT-Discover scores 567,062, surpassing the top human score of 566,997, and in Scheduling, it scores 848,414,228, exceeding the best human score of 847,674,723.

Results show that TTT-Discover achieves state-of-the-art performance across all GPU types in the TriMul competition, outperforming the best human submissions by over 15% on average. The method produces kernels that are significantly faster than existing human and AI baselines, with the best kernel on H100 running at 1161.2 microseconds, surpassing the top human result by 22%.